Имеется иное представление рационального числа 1/2, отличное от представлений вида 2/4, 3/6, 4/8 и т. д. Мы подразумеваем представление в виде десятичной дроби 0,5. Одни дроби имеют конечные десятичные представления, например,

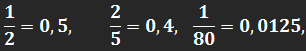
в то время как десятичные представления других дробей бесконечны:

Эти бесконечные десятичные дроби можно получить из соответствующих рациональных дробей, деля числитель на знаменатель. Например, в случае дроби 5/11, деля 5,000... на 11, получаем 0,454545... .

Какие рациональные дроби a/b имеют конечные десятичные представления? Прежде чем ответить на этот вопрос в общем случае, рассмотрим конкретный пример. Возьмем, скажем, конечную десятичную дробь 8625. Мы знаем, что

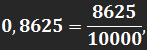
и что любая конечная десятичная дробь может быть записана в виде рациональной десятичной дроби со знаменателем, равным 10, 100, 1000 или какой-либо другой степени 10. Приводя дробь справа к несократимой дроби, получаем

Знаменатель 80 получен делением 10 000 на 125 — наибольший общий делитель 10 000 и 8625. Поэтому в разложение на простые множители числа 80, как и числа 10 000, входят только два простых множителя: 2 н 5. Если бы мы начинали не с 0,8625, а с любой другой конечной десятичной дроби, то получившаяся несократимая (Рациональная дробь а/b называется несократимой, если целые числа а и b не имеют общего делителя, большего чем 1) рациональная дробь а/b тоже обладала бы этим свойством. Иначе говоря, в разложение знаменателя b на простые множители могли бы входить лишь простые числа 2 и 5, поскольку b есть делитель некоторой степени 10, а 10 = 2∙5. Это обстоятельство оказывается определяющим, а именно имеет место следующее общее утверждение:

Несократимая рациональная дробь а/b имеет конечное десятичное представление тогда и только тогда, когда число b не имеет простых делителей, отличных от 2 и 5.

Отметим, что при этом b не обязано иметь среди своих простых делителей оба числа 2 и 5: оно может делиться лишь на одно из них или не делиться на них вовсе. Например,

здесь b соответственно равно 25, 16 и 1. Существенным является отсутствие у b других делителей, отличных от 2 и 5.

Сформулированное выше предложение содержит выражение тогда и только тогда. До сих пор мы доказали лишь ту часть, которая относится к обороту только тогда. Именно мы показали, что разложение рационального числа в десятичную дробь будет конечным лишь в том случае, когда b не имеет простых делителей, отличных от 2 и 5. (Иными словами, если b делится на простое число, отличное от 2 и 5, то несократимая дробь а/b не имеет конечного десятичного выражения.)

Та часть предложения, которая относится к слову тогда, утверждает, что если целое число b не имеет других простых делителей, кроме 2 и 5, то несократимая рациональная дробь а/b может быть представлена конечной десятичной дробью. Чтобы это доказать, мы должны взять произвольную несократимую рациональную дробь а/b, у которой b не имеет других простых делителей, кроме 2 и 5, и убедиться в том, что соответствующая ей десятичная дробь конечна. Рассмотрим сначала пример. Пусть

Для получения десятичного разложения преобразуем эту дробь в дробь, знаменатель которой представляет собой целую степень десяти. Этого можно достигнуть, умножив числитель и знаменатель на 5⁵

Приведенное рассуждение можно распространить на общий случай следующим образом. Предположим, что b имеет вид 2^m*5^m, где m и n — неотрицательные целые числа (т. е. положительные числа или нуль). Возможны два случая: либо n меньше или равно m (это условие записывается n≤m), либо n больше m (что записывается n>m). При n≤m умножим числитель и знаменатель дроби на 5^m-n:

Поскольку целое число m-n не отрицательно (т. е. положительно или равно нулю), то 5^m-n, а следовательно, и a*5^m-n — целое положительное число. Положим a*5^m-n=c. Тогда

Но деление целого числа на 10^m сводится просто к постановке запятой на соответствующем месте в десятичном представлении этого числа. Поэтому мы получим конечную десятичную дробь.

Во втором случае, когда n>m умножим числитель и знаменатель дроби a/b на 2^n-m

Отсюда, обозначив целое число a*2^n-m через d, по­лучаем

Таким образом, здесь, как и в первом случае, мы приходим к конечной десятичной дроби.